BENT PYRAMID



(Designed by Samuel Laboy)
The Bent Pyramid was built in Dahshur, Egypt, by pharaoh Sneferu, father of Pharaoh Khufu, builder of the Great Pyramid. The Bent Pyramid is better known by its two different angles in its inclined sides. Egyptologists indicates that this Pyramid was under construction, when its initial angle had to be changed; up to the pyramid’s top, as necessary to repair a faulty design of the Egyptian engineers, or by the failure of the structure.
For Engineer Samuel Laboy, from Puerto Rico, this is a simplistic solution which buries well underground one of the most important and historic pyramids design in Egypt. To solve this design, he used the Perfect Symbol system, previously used by him to solve the geometric design of the Great Pyramid, and others. He found that the Bent Pyramid shape is composed of the superimposition of two important and unique pyramid’s designs. He explains that the reasons for the pyramid combined design could be, from the spiritual point of view of the Egyptians, to provide with this new geometric arrangement, a powerful and energetic force to the pyramid.
As a professional Civil Engineer, Laboy do not accept the theories elaborated to explain the changes in the angles. He believes the pyramid was designed and built as iconstructed. He said that the two geometric configurations, when superimposed, using an equal scale, create a combined configuration exactly equal to that of the Bent Pyramid.
The following is the method Engineer Laboy used to rescue and to determine the Bent Pyramid’s design. He states that this is not a theory, if he said so, he would be lying. The fact that all calculations, properties and characteristics, exactly fit the design, like he did with the Great Pyramid geometric design, is irrefutable evidence of it exactness, and proves that this is another very important discovery for the Egyptology world.
As he explained, demonstrated and illustrated in his new books “A Civil Engineer looks at the Great Pyramid” and its “Supplement”, the Bent Pyramid follows a geometric pattern composed of two completely different geometrical configurations. Each configuration has a particular reason to be incorporated in the Bent Pyramid’s design.
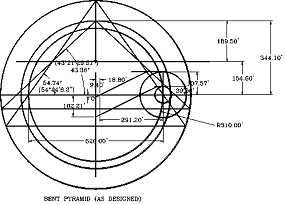
The first model establishes the lower angle of the Bent Pyramid. Its configuration represents the pyramid that is created with the well-known configuration of a square circumscribed by a circle. He said that this would be the simplest pyramid’s design model of a pyramid. The tangent of the slope of this pyramid is equivalent to the square root of two (√2). Therefore, the corresponding angle for this slope is 54° 44’ 8.197”, and as it is known, this is the correct angle for the lower section of the Bent Pyramid.
The second pyramid’s model, when superimposed over the first, shows the upper angle of the Bent Pyramid. This pyramid has an important and special configuration. In this case is one of the most elaborated, complicated and amazing configuration for a pyramid. It seems that the designer is including in the Bent Pyramid’s design the complete range of pyramid designs, from the simplest to the most elaborated. Laboy explained that he classified this pyramid in his main book, in Chapter 10, as type VI, the special case, “when the construction circle is located inside the base of the pyramid”. In this particular case, the perimeter (P) of the pyramid’s base is equal to the diameter of the circle multiplied by Phi cubed (=Df³). When the cross sectional views of both model pyramids are superimposed under equal scales, the cross sectional view of the Bent Pyramid, emerges.
About the Phi function = f = 1.618033989..., is given by our Creator as a proportioning parameter in the micro and macro cosmos. It appears in human proportions, as illustrated by Leonardo Da Vinci in his famous human proportion’s drawing, in some animal bodies-shapes, even in the shapes of the expanding galaxies in the cosmos. Its decimal numbers never ends, as the function of Pi =p= 3.1415926…, .
The Phi function number (f) is easy to construct using mathematical series, from a square figure, even from a circle. He discovered that the right triangle with sides in the proportion 1:2 is a (Phi function generator). This simple triangle, easily set with three nails and a chord, will provide the solution, or answers, to practically all (f) combinations. This method could have been the ancient (Egyptian-computer) to work out the f functions. However, as known, and experienced by me, Egyptologists have banned the Phi function, and the circle configuration from the pyramid’s studies, and what are really are doing is closing the entrance doors to the pyramid’s geometrical solution.
As a side note, apparently, the Phi cubed (= f³) was very important for the Egyptian works. It was used to build the Red Pyramid and the top of the Bent. This relation is so important in geometry and Maths, that there is no doubt that the Egyptian designers knew about it and used it to strengthen, or give power to their construction works.
The ratio of the circle’s diameter and the pyramid’s side length (= D / b), represents the function of the tangent of the angle of the face for a pyramid. For example, in the upper section of the Bent Pyramid, this ratio is equivalent to 4 divided by (f³) = 0.94427191. Therefore, the angle corresponding to this tangent’s function is 43° 21' 29.51", exactly the same angle measured at the upper section of the Bent Pyramid.
From another point and very important, apparently, Pharaoh’s Chephren knew very well about the two angles which formed the Bent Pyramid's structure, He considered them so important that for his pyramid in Giza, he used the combination of the two slope angles which composed the Bent pyramid's structure. Therefore, he multiplied the (square root of 2) = (2)corresponding to the lower section, by 4 divided by (f³) for the upper section. The resulting slope is 1.335402142, which gives the angle 53.17273225° = 53° 10’ 21.83. This is the angle used for his pyramid at Giza.
From another point, Engineer Laboy found and explains in his books how to set the descending passages for the pyramids. Using his geometrical method and the Perfect Symbol, he designed, independently, the descending passage of each of the two pyramid's models of the Bent Pyramid. Therefore, both passages were also superimposed in his Bent Pyramid’s geometric design. He found that the cross section of the pyramid corresponding to the lower section of the Bent Pyramid was set from south to north, therefore, the entrance door is at the north; while the pyramid’s design for the second pyramid, was superimposed from east to west, therefore, the entrance door is located at its west side. Both his designed descending passages corroborate the two descending passages lengths and elevation built for the Bent Pyramid. It is remarkable that the designed passages by Laboy and and the constructed at the Bent Pyramid’s structure, illustrate the same entrance location and elevation.
Laboy concluded that the superimposition of one pyramid's model design, over the other, creates the two angles shown by the Bent Pyramid. In his model, the vertical distance from the pavement to the change in angle elevation, was calculated as 154.60 ft. As a matter of fact, this is the vertical distance measured at the Bent Pyramid's structure between these two points. In addition, the descending passages and entrance doors, and other calculated dimensions, angles, and lengths are exactly equal to those measured by surveyors at the Bent Pyramid’s structure. We do not need an old papyrus to tell us that his designed plan corresponds to the Bent Pyramid. He said: "Egyptologists can read hieroglyphs, Engineers can read structures".
It is interesting to examine the special case of the Red Pyramid and the upper section of the Bent Pyramid. The ratio between the circumference of the circle and the perimeter of the square (C / P) is equivalent to (p / f³). Note that the perimeter of the square base is equal to the diameter of the circle multiplied by f³, or P = D f³, and also that the radius R = 2 (b) / f³.
That is, the ratio (C / P) = p D / 4 (b) = p D / P = p D / D f³, which finally shows that (C / P) = (p / f³). Having (C / P) = (p / f³), it can be established that the perimeter (P) of the square base for this pyramid would be equal to the diameter (D) of the circle, multiplied by f³, that is, P = D f³, and that R = pyramid’s height = 2 (b) / f³.
I am sure that all of these math's and geometry can be understood by Egyptologists, or can be referred to their favorite Universities for verification. They are irrefutable evidence of the great knowledge in those sciences of the Ancient pyramid builders. We should not negate this ancient Culture their great knowledge in this sciences because they did not left and easy to find papyrus, to prove it. However, they left their extraordinary works to prove that they did them.