
Red Pyramid
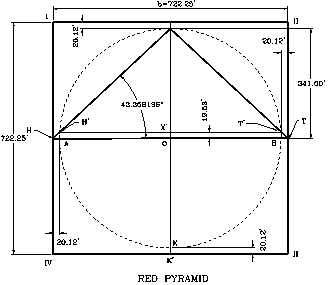
Figure 207
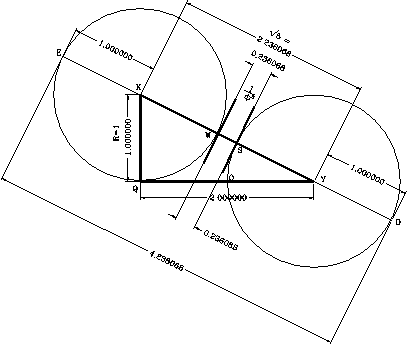
Figure 209
Since the Red Pyramid has the same configuration used for the upper section of the Bent pyramid, we can take a good look to it. The Red Pyramid is located about 1 mile to the north of the Bent Pyramid. The slope angle for this Pyramid, although indicated as 43° 22' by the references, should be also 43° 21' 30". As already said, this angle is supposed to represent the angle from the designed plans, and could vary slightly from the angle built and measured in the structure. The references indicate that the Red Pyramid’s height is about 341 feet, and the base length about 722 feet.
Therefore, using the slope angle of 43° 21' 30" for the configuration of the Red Pyramid, its design could be explained showing the corresponding measurements. The same formulas apply to both configurations. Therefore, since the Red Pyramid’s side length are approximately 722 feet, then, the pyramid’s height, using my formula, would be equal to h = R = (2b) / f) = (2)(722) / f³ = 341 feet. Nevertheless, as explained, due to the poor accuracy in its construction, and deterioration through the ages, we might find a slight variation. In this case, the side's length is correct.
Figure 207
I believe and suggest that the scholars should further investigate the timetable of the Red and Bent Pyramid construction. According to the use of the geometrical configurations, it seems that the construction of the Red Pyramid proceded that of the Bent Pyramid, contrary to the opinion of scholars that indicate that the Bent Pyramid was built first. The fact that Red Pyramid’s configuration was used superimposed with another configuration to design the Bent Pyramid suggests that it was first used in the Red Pyramid, and afterwards, combined in the Bent Pyramid.
From another point, I made so much reference to the value of f³ and its inverse, (1 / f³), in the geometrical configuration formulas for the upper section of the Bent Pyramid, the Red Pyramid, and also present in the Great Pyramid’s design, that it deserves a more detail explanation on my part.
The value of (1/f³) is present in the formula (D/b) = 4/ f³ and in the ratio of the circumference of the circle to the perimeter of the square base, that is, C/P = p/f³. Its length can be easily traced geometrically using a triangle with sides in the proportion 1:2, as shown in the figure.
The figure shows a right triangle between points Q, K, and Y, having its sides opposite to the hypotenuse in the ratio 1 : 2. The short side (QK) is equal to 1, and the long side (QY) is equal to 2. With center at K, trace a circle with radius equivalent to QK (= 1). Then with center at Y, trace another circle with an equal radius.
The distance between the intersection points of the two circumferences with the hypotenuse (KY) represents the value of (1 / f³). This distance is identified between the points (W) and (S). Since QKY is a right triangle, having its short side KQ = 1, and the long side QY = 2, by means of the Pythagorean theorem, the hypotenuse KY is equal to Ö5. Therefore, segment (WS) of the hypotenuse will be equal to (Ö5 -2), that is, the length of the hypotenuse, less the radius of the circles with centers at K and Y. Consequently, the value of (Ö5 -2) = 0.236067978 = (1 / f³).
Figure 209 shows a detailed drawing illustrating both the relation between (1 / f³), f³, with the Red Pyramid, Bent Pyramid, and Great Pyramid’s configuration. The drawing is composed of a base circle with center O and radius R = 1. In addition, the drawing shows the basic Great Pyramid’s configuration as illustrated between points P, Q, and N (the slope angle of the pyramid is equal to 51.82729°).
The drawing also shows four geometrically interlaced circles of equal radius, with centers at Q, Y, B and K. The side QY of the triangle QYK is set equal to R = 1, while its side QK = 2 (R) = 2. The hypotenuse KY, using the Pythagorean theorem, is equal to Ö5 (R) = Ö5. \
From the formulas, the Red Pyramid side lengths are equivalent to (b) = f³/ 2. This (b) value represents half (= 1/2) the length of the line ML (= f³). This means that the perimeter of the base of the Red Pyramid is equivalent to the product of 2(R) multiplied by f³. In other form, P = (4b) = (2) f³. From another point, since the function of the function of the tangent of the slope is defined by the ratio (D / b) = 4 / f³, it means that the function of the angle is equally defined by the product of (4) multiplied by the length of WS.
Figure 208
The distance WS, between the points where the circumferences of circles with centers K and Y cut the line ML, is equal to the square root of 5, less 2, times (R). That is, (Ö5 - 2)(R) = (1 / f³). To facilitate the identification of WS, I showed its length, equivalent to the diameter of the small circles in the drawing.
Figure 209
If the length of the line ML is analyzed, it can be observed that it is equivalent to 4 radiuses (= 2 diameters), plus its segment WS. Expressed as a formula, the length of line ML = 4 (R) + (1/f³) (R). When R = 1, the formula is reduced to ML = 4 + (1/f³), value that is also equivalent to f³. Therefore, in this configuration the total length of the line ML represents f³, while its segment WS, represents the inverse value of f³, that is, 1 / f³. Observe that (f³-1 / f³) = 4, and by transposition, f³= 4 + (1 / f³).
If the radius is made equal to 480.6637 feet, that is, the Great Pyramid’s height, the length of the line ML = 480.6637 ( f³) = 2,036.12 feet. The value of WS = (480.6637) (1 / f³) = 113.47 feet. However, if the radius is 341 feet (the Red Pyramid’s height), ML = 341 ( f³) = 1,444.4992 feet and (b) = 1,444.4992 / 2 = 722.2496 feet. As shown in the figure, if the length WS = (1/ f³) (R), is projected into the section of the drawing that shows the Great Pyramid’s configuration between points P, Q, and N. It will be noticed that WS is equivalent to the vertical distance at which point X in the vertical axis, is located underneath the base of the pyramid, that is, 113.47 feet, when R = 480.6637 feet.
All of these calculations, geometrical configurations, mathematical and geometrical relations, ratios, and formulas, directly connect the geometry of the Red, the Bent and the Great Pyramid, as well other pyramids. They are mathematical evidence that the Bent Pyramid configuration is not product of a pyramid failure or change in plans because of its instability. This mathematical evidence will be here, as revealed, and when new archeological discoveries exposed the truth, I am sure there will be one flag waiving in the air.

Red Pyramid
