Figure 191
The Pyramid of Mycerinus is the smallest of the three great pyramids. It is 213.90 feet height and side’s length about 343 feet. The geometrical configuration of this pyramid seems to be the most simple of all. Nevertheless, the architect or engineer gave all of us a lesson in Geometry with his design. The pyramid’s configuration is based on the ratio of its side’s length (b) and its height (R), which is equal to Phi (1.6180339), that is, b / R = f. In other words, the sides (b) of the pyramid are equal to the product of its height (R) and the Phi (f) value, b = Rf This geometric configuration was discussed and illustrated in Chapter 6. It is part of the drawing used by Leonardo da Vinci to illustrate the human’s body proportions by using the superimposed figures of a man inside the circumference of a circle and inside the perimeter of a square (also shown in figure 191).
Figure 191
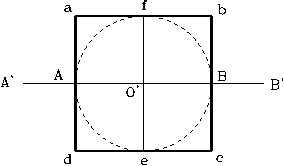
In Leonardo’s drawing, the figure of the circle corresponds to the man when his hands are raised to the top of his crown and his legs are apart, while the square corresponds to his figure when the body is erected, his feet on the floor, and his hands horizontally stretched to the sides.
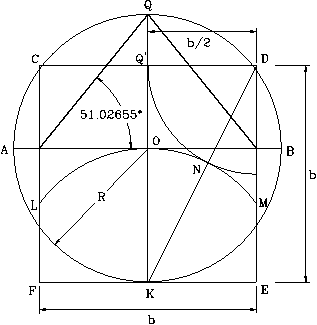
The base of the Pyramid of Mycerinus corresponds to the square shown in the figure between points C, D, E, and F. The tangent of the slope of the pyramid is (D / b) = D / (R) f = (2)R / (R) f = 2 / f =1.236067978. The angle corresponding to this slope is 51.026555266° (51° 01' 35.59".
The process to trace the geometrical configuration corresponding to the Pyramid of Mycerinus, using this mentioned configuration is as follows:
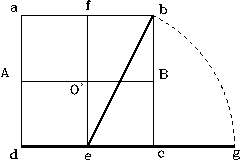
1. Trace a line of length A’ B’, oriented north. Select a point (O’) in the line A’ B’, as shown in figure 192. From point O’, trace a circle of any convenient radius for the drawing, and circumscribe a square (abcd) to the circle. Mark points A and B at the intersection of the vertical sides of the square with the horizontal line A’ B’. Trace the vertical line (fe) from the midpoint of sides (ab) to the midpoint of the line (dc) of the square. The distance between point A and B corresponds to the circle’s horizontal diameter, and the vertical line (fe) to the vertical diameter.
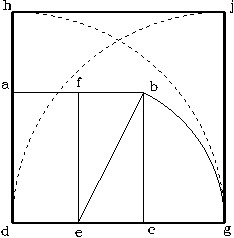
2. As shown in figure 193, with point (e) as center, and (eb) as radius, trace an arc to cut the extension of the side (dc) of the square. Mark the intersection as point (g).
Figure 193
3. Then, as shown in figure 194, with point (d) as center, and (dg) as the radius, trace an arc to intercept the extension of the side (da) of the square. Mark point (h) at the intersection. Then, from point (g), and radius (gd) trace another arc to intercept the vertical line through point (g). Mark point (j) at the intersection. Join points (h) and (j) to complete another larger square (hjgd), which will represent the square base of the Pyramid.
Figure 194
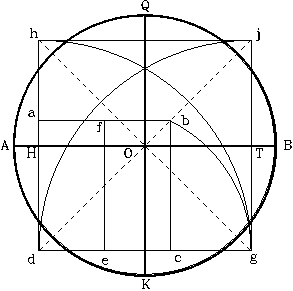
4. Following with figure 195, trace the diagonals (dj) and (hg) to the square (hjgd), and mark point O at their intersection. With point O as center, trace the circumference of another circle, using as its radius an equivalent length to one of the sides of the square (abcd).
Figure 195
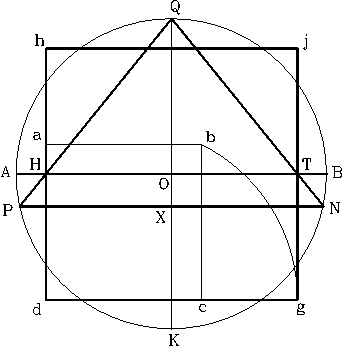
Trace the vertical diameter QK and the horizontal AB, to this circle. Establish point H at the intersection of the horizontal diameter and side (dh) of the square (hjgd). Established point T, at its intersection with side (gj), of the same square.
5. Trace a line from point Q to point H and extend it to intersect the circumference, as shown in figure 196. Define point P at the intersection. Trace another line from point Q to point T, and extend it to intersect the circumference. Mark point N at its intersection. Trace a line to join points P and N. Mark point X at the intersection of line PN with the vertical diameter.
Figure 196
In figure 197, the triangle HQT represents the vertical cross section of the pyramid structure as seen through the center of its faces. The distance from point H to point T represents the length of the pyramid’s sides. Line HT, a segment of the horizontal diameter AB, also identifies the base of the pyramid and the surface of the terrain where it will be built. The inclined distances HQ and QT represent the apothem of the pyramid.
The four intersection points identified as (h) (j), (g), and (d) establish the location of the projection of the four corners of the square base of the pyramid. The big triangle formed between points Q, P, and N, defines the vertical cross section of the pyramid, as seen through the center of their faces, including its underground section. The section PHTN represents the area, underneath the base of the pyramid, where the underground corridors and chambers will be constructed.
Figure 197
After the geometric design is finished, the value and unit of measurement for its height will be set. All other dimensions will be proportional to the established pyramid’s height.
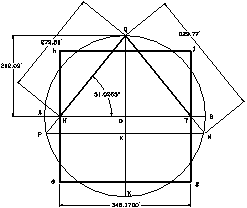
As I already stated, the ratio between the length’s side and the height of the Pyramid of Mycerinus, represents the Golden Number. That is, b / R = f. This formula can be re-arranged to R = b / f. This means that with a side length equivalent to 343 feet its height would be R= h = 343.17 / f = 212.09 feet. Since the side’s length and the height of the pyramid are known, the pyramid is defined. Figure 197 shows the calculated dimensions for the design.
The data reported by Sir W. M. Flinders Petrie for this Pyramid, shows that the results of my calculations for the shown design are within acceptable limits, and could be considered correct.
Calculated dimensions
Pyramid’s height = R = h = 212.09 feet Length of the sides = b = f (R) = 343.17 feet
Tangent of angle q = (D/b) =2 (R) / f (R) =2 / f= (Ö5-1) = 1.23607.
Angle of slope= q = 51.02655° = 51° 01' 35.59"
tan q = (D/b)= (212.09) (2)/343.17 = = 1.23607 = (Ö5-1)
Dimensions of the Pyramid of Mycerinus: According to Sir W. M. Flinders Petrie’s Survey (1881-82)
Pyramid’s height = R = h = 2,564 inches (213.67') - (more or less 15 inches)
Correct value is between = 212.42 to 214.92 feet
Length of the sides = b = 4,153.6 inches = 346.13 feet
Angle of slope = 51° 00' (more or less 10')